【投資の基本】単利と複利の違いをしっかりとまとめました

単利、複利は投資の利回りの種類です。単利は投資額にのみ利子がつき、複利は投資額に対して得られた利子を再投資することにより、次に受け取る利子を増やします。投資の勉強を本格的に行おうと思い、まずは単利、複利の違いをしっかりとまとめました。

単利と複利の増え具合

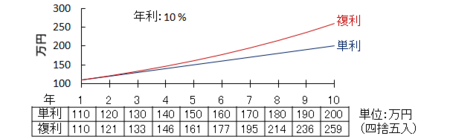
今、100万円持っているとします。この100万円を年利10％で運用することを考えます。このとき、単利、複利のそれぞれでの資産の増え具合は上図のようになります。

単利は常に100万円に対して10％の利益が得られます。それに対して複利は、例えば2年目の利益は1年目の総資産である110万円に対して得られます。利益を運用に組み入れるか組み入れないかで、10年目には約59万円の差がつきます。

単利の原理

時刻 $t_0$ において投資額 $S_0$ を投資します。この投資は時刻 $t_n$ までに単利での利子が $n$ 回得られるとします。また、簡単のため、利子が得られる間隔は均等で $T$ とし、単位時間あたりの利子率は時間に依存せず一定で $R$ とします。このとき、 $t_n$ における回収額 $S_n$ と $S_0$ との関係は次式で表されます。

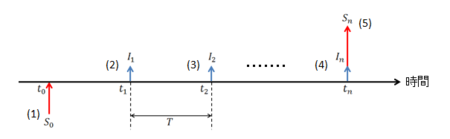
$S_n=(1+nTR)S_0$ 　(A)

導出は次の通りです。まず、 $t_0$ において、 $S_0$ を何かに投資したとします(1)。この投資は $t_1$ においてに $S_0$ 対する利子 $I_1$ を得ます(2)。同様に、 $t_2$ において $S_0$ に対する利子 $I_2$ (3)、 $t_n$ において $S_0$ に対する利子 $I_n$ を得ます(4)。利子率が均等であることを考慮すると、 $I_1$ 、 $I_2$ 、...、 $I_n$ はすべて等しいため、それらの関係は、

$I_1=TRS_0(=I_1=I_n)$

となります。そして、 $t_n$ における $S_n$ は、 $S_0$ と $I_1$ 、 $I_2$ 、...、 $I_n$ との加算です(5)。上式を考慮すると、式(A)は以下のように導出されます。

$S_n=S_0+S_1+S_2+...+S_n\,\cdots\\\hspace{9pt}=S_0+TRS_0+TRS_0+...+TRS_0\,\cdots\\\hspace{9pt}=(1+nTR)S_0$

複利の原理

単利と同様に、時刻 $t_0$ において投資額 $S_0$ を投資します。ただし、この投資は時刻 $t_n$ までに複利での利子が $n$ 回得られるとします。また、 $T$ 、 $R$ はそれぞれ利子が得られる間隔、単位時間あたりの利子率を表します。このとき、 $t_n$ における回収額 $S_n$ と $S_0$ との関係は以下の式で表されます。

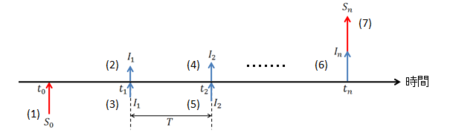
$S_n=(1+TR)^nS_0$ 　(B)

導出は次の通りです。まず、時刻 $t_0$ において、投資額 $S_0$ を何かに投資したとします（1）。この投資は $t_1$ において $S_0$ に対する利子 $I_1$ を得ますが(2)、得られた $I_1$ はすぐに再投資します(3)。 $t_2$ においては $S_0+I_1$ に対する利子を得て(4)、すぐに再投資します(5)。つまり、 $t_1$ 、 $t_2$ 時点における $S_0+I_1$ 、 $S_0+I_2$ は、

$S_0+I_1=(1+TR)S_0$
$S_0+I_2=(1+TR)(S_0+I_1)\,\cdots\\\hspace{27pt}=(1+nTR)S_0=(1+TR)^2S_0$

となります。同様の手順で、 $t_n$ における $S_0$ と $I_n$ (6)との和は $(1+TR)^nS_0$ となり、この式は $S_n$ (7)に相当します。　

単利と複利の比較

$t_n$ における単利、複利の回収額 $S_n=(1+nTR)S_0$ 、 $S_n=(1+TR)^nS_0$ の利子率が関わる項、

$(1+nTR)$
$(1+TR)^n$

を比較します。まず、 $n$ を変化させたときの $S_n=(1+nTR)$ 、 $S_n=(1+TR)^n$ を下図に示します。ただし、 $T=1$ とし、 $R=0.01$ 、 $0.03$ を想定しました。青、赤はそれぞれ単利、複利であり、破線、実線はそれぞれ $R=0.01$ 、 $0.03$ を示しています。

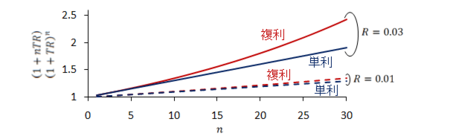
$n$ が大きくなるにつれ、単利と複利との乖離が明確に表れているように思えます。また、 $n=30$ において、 $R=0.01$ のとき、 $S_n=(1+TR)^n$ は $S_n=(1+nTR)$ の約1.037倍となり、 $R=0.03$ のときは約1.278倍と計算されます。つまり、 $R$ によって単利と複利との乖離度合が決定されると考えられます。横軸に $R$ をとり、縦軸に $(1+TR)^n/(1+nTR)$ をとった結果を下図に示します。

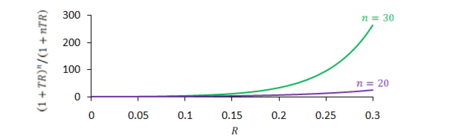
$R=0.03$ において、 $n=20$ で運用すると複利は単利の約27倍となり、 $n=30$ で運用すると約262倍となります．

複利の限界

複利において、再投資の間隔と複利の最終的な利子率との関係を考えます。つまり、例えば、運用期間を10年と設定したとき、利子を受け取って再投資する間隔が1年と1ヵ月ではどのような違いがでるか、といった問題を考えます。

再投資の間隔は $(t_n-t_0)/n$ とも書けるため、複利の利子率に関わる項 $(1+TR)^n$ は $(1+(t_n-t_0)R/n)^n$ と表されます。この $n$ を大きくしていくと、ネイピアの定義により、

$\displaystyle \lim_{n \to \infty}(1+(t_n-t_0)R/n)^n=\mathrm{e}^{(t_n-t_0)R}$

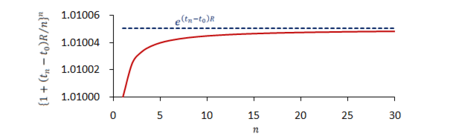
となります。つまり、どんなに再投資間隔を短くしていっても最終的な利子率は $\mathrm{e}^{(t_n-t_0)R}$ 以上にはならないことを表しています。例として、 $(t_n-t_0)/n$ 、 $R=0.01$ としたときの $n$ に対する利子を以下に示します。青の破線は最終的な利子率を示しています。